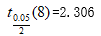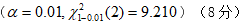首页 考试大纲 详情页

 目录

I、 学科性质和学习目的………………………………………………………………………2

II、课程内容与考核目标………………………………………………………………………2

第一章、随机事件及其概率………………………………………………………………2

第二章、随机变量及其分布………………………………………………………………3

第三章、随机变量的数字特征……………………………………………………………5

第四章、随机抽样及抽样分布……………………………………………………………6

第五章、抽样估计…………………………………………………………………………7

第六章、假设检验…………………………………………………………………………8

III. 考试形式及试卷结构………………………………………………………………………9

IV. 参考书目……………………………………………………………………………………9

V.  题型示例……………………………………………………………………………………9

全国高等教育自学考试药学专业（独立本科段）

《数理统计》考试大纲

专业代码：B100805   课程代码：3049

I、 学科性质和学习目的

概率论与数理统计是研究随机现象的数量规律性的一门学科。在医学、药学及卫生科技工作中有着广泛的应用。根据医学、药学、卫生及生物医学工程科研工作的实际需要，结合医药科技的实际背景，考生通过参加考试，应基本了解或理解“概率论与数理统计”中随机事件及概率，随机变量及其分布，随机变量的数字特征，随机抽样与抽样分布， 参数估计与假设检验等基本内容中的概念和理论；理解或掌握上述各内容中的有关方法；能运用所学知识分析并解决简单的实际问题。

II、课程内容与考核目标

第一章、随机事件及其概率

一、学习目的和要求

通过本章的学习, 了解随机试验、古典概型、事件间的关系与运算、完备事件组、事件的频率、概率的统计定义、事件的独立性等概念, 掌握随机事件的定义及表示、概率的古典定义及计算、概率的加法公式及应用、条件概率的定义、概率的乘法公式及应用、全概率公式、贝叶斯公式及其应用。

二、课程内容

               第一节  随机事件及其运算

(一)随机事件的定义，基本事件与样本空间。

(二)事件间的关系与运算，完备事件组。

第二节  随机事件的概率

(一)事件的频率，概率的统计定义，事件概率的基本性质。

(二)古典概型，概率的古典定义，事件概率的计算。

第三节  概率的基本运算法则

(一)概率的加法公式。

(二)条件概率，概率的乘法公式，事件的独立性。

第四节  全概率公式与逆概率公式

(一)全概率公式和贝叶斯公式。

(二)独立重复试验。

三、考核知识点和要求

（一）随机事件及其运算

识记：随机事件的定义，基本事件与样本空间，事件间的关系与运算，完备事件组。

（二）随机事件的概率

识记：事件的频率，古典概型事件。

领会：概率的统计定义，概率的基本性质。

应用：概率的古典定义及事件概率的计算。

(三) 概率的基本运算法则

领会：条件概率和事件的独立性。

应用：概率的加法公式和概率的乘法公式。

（四）全概率公式与逆概率公式

识记：独立重复试验。

应用：全概率公式和贝叶斯公式及其计算。

第二章、随机变量及其分布

一、学习目的和要求

通过本章的学习, 了解随机变量、分布函数、随机向量、随机变量函数的分布等概念, 掌握离散型随机变量的概率函数、连续型随机变量的概率密度函数、常见的离散型随机变量的分布。

二、课程内容

第一节 随机变量与离散型随机变量的分布

（一）随机变量的定义。

（二）离散型随机变量的概率函数及性质。

（三）随机变量的分布函数及性质。

第二节、常见的离散型随机变量的分布

• 超几何分布，0—1分布(两点分布)和二项分布。

（二）泊松(Poisson)分布。

第三节、连续型随机变量的分布和常见的连续型随机变量的分布

（一）连续型随机变量的概率密度函数。

（二）均匀分布，正态分布和标准正态分布*，指数分布。

第四节、随机向量

（一）二维离散随机向量及其分布列。

（二）边缘分布与条件分布。

（三）二维连续随机向量及其概率密度函数。

（四）边缘密度与条件密度。

第五节、随机变量函数的分布

常见的二维随机变量的分布。

三、考核知识点和要求

（一）随机变量与离散型随机变量的分布

识记：随机变量的定义。

领会：离散型随机变量的概率函数，随机变量的分布函数

应用：离散型随机变量概率函数的性质，随机变量分布函数的性质。

（二）常见的离散型随机变量的分布

识记：超几何分布，0—1分布(两点分布)和二项分布的定义，泊松(Poisson)分布的定义。

应用：超几何分布的概率计算，0—1分布(两点分布)和二项分布的概率计算，泊松(Poisson)分布的概率计算。

（三）、连续型随机变量的分布和常见的连续型随机变量的分布

识记：连续型随机变量的概率密度函数。

领会：均匀分布，正态分布和标准正态分布，指数分布等的定义。

应用：均匀分布，正态分布和标准正态分布，指数分布等的概率计算。

（四）、随机向量

识记：二维离散随机向量及其分布列，边缘分布与条件分布。

领会：二维连续随机向量及其概率密度函数，边缘密度与条件密度。

（五）、随机变量函数的分布

识记：常见的二维随机变量的分布。

第三章、随机变量的数字特征

一、学习目的和要求

通过本章的学习, 了解随机变量的数字特征，分位数，临界值等概念, 掌握数学期望的定义，方差的定义，常见离散型随机变量分布的数字特征，常见连续型随机变量分布的数字特征。

二、课程内容

第一节、数学期望

（一）随机变量的数学期望(均值)的定义。

（二）数学期望的性质。

（三）常见的离散型随机变量分布的数学期望。

（四）常见的连续型随机变量分布的数学期望。

第二节、方差、协方差和相关系数

（一）随机变量的方差、标准差的定义。

（二）随机变量的协方差和相关系数的定义。

（三）方差的性质。

（四）常见的离散型随机变量分布的方差。

（五）常见的连续型随机变量分布的方差。

三、考核知识点和要求

（一）、数学期望

识记：随机变量的数学期望(均值)的定义。

领会：数学期望的性质。

应用：常见的离散型随机变量分布的数学期望，常见的连续型随机变量分布的数学期望。

（二）、方差、协方差和相关系数

识记：随机变量的方差、标准差的定义，随机变量的协方差和相关系数的定义。

领会：方差的性质。

应用：常见的离散型随机变量分布的方差，常见的连续型随机变量分布的方差。

第四章、随机抽样及抽样分布

一、学习目的和要求

通过本章的学习, 了解随机抽样的方法，了解样本频率直方图，样本累积频率函数图的概念。掌握随机抽样的有关概念（总体，个体，样本，统计量，样本数字特征等），掌握抽样分布的有关结论。

二、课程内容

第一节、抽样的基本概念和方法

（一）总体和个体。

（二）简单随机样本和统计量，样本的数字特征。

（三）随机抽样的方法。

第二节、样本分布图

（一）样本频率直方图。

（二）样本累积频率函数图。

第三节、抽样分布

（一）样本均值的分布及有关结论。

（二）分布的定义及有关结论。

（三） t分布的定义及有关结论。

（四） F分布的定义及有关结论。

三、考核知识点和要求

（一）、抽样的基本概念和方法

识记：总体和个体，随机抽样的方法。

领会：简单随机样本，统计量。

应用：样本的数字特征。

（二）、样本分布图

识记：样本频率直方图，样本累积频率函数图。

（三）、抽样分布

识记：样本均值的分布，分布的定义，t分布的定义，F分布的定义。

领会：样本均值的分布的有关结论，分布的有关结论， t分布的有关结论， F分布的有关结论。

第五章、抽样估计

一、学习目的和要求

通过本章的学习, 掌握点估计的概念和特性，掌握区间估计的概念，了解点估计的顺序统计量法和矩估计法，掌握点估计的数字特征法和最大似然估计法。掌握正态总体期望值的区间估计，掌握正态总体方差的区间估计，掌握两个正态总体期望值差及方差比的区间估计。了解二项分布和泊松分布总体参数的区间估计。

二、课程内容

第一节、抽样估计的概念

（一）点估计的概念和三个特性。

（二）区间估计的概念。

第二节、总体参数的点估计

数字特征法，顺序统计量法，矩估计法，最大似然估计法。

第三节、正态总体参数的区间估计

（一）正态总体期望值的区间估计。

（二）正态总体方差的区间估计。

（三）两个正态总体期望值差及方差比的区间估计。

第四节、二项分布和泊松分布总体参数的区间估计

精确估计方法，大样本正态近似法。

三、考核知识点和要求

（一）、抽样估计的概念

识记：点估计的概念。

领会：点估计的三个特性，区间估计的概念。

（二）、总体参数的点估计

识记：顺序统计量法，矩估计法。

领会：数字特征法，极大似然估计法。

（三）、正态总体参数的区间估计

领会：两个正态总体期望值差及方差比的区间估计。

应用：正态总体期望值的区间估计，正态总体方差的区间估计。

（四）、二项分布和泊松分布总体参数的区间估计

识记：精确估计方法，大样本正态近似法。

第六章、假设检验

一、学习目的和要求

通过本章的学习，了解假设检验的原理----小概率原理，掌握假设检验的一般步骤，了解假设检验的两类错误。掌握假设检验的常用方法（置信区间法，临界值法，P值法）。掌握正态总体期望值的假设检验（u检验，t检验）。掌握正态总体方差的假设检验（检验，F检验）。了解列联表资料的检验。

二、课程内容

第一节、假设检验的基本思想

（一）小概率原理和两类错误。

（二）假设检验的一般步骤，

第二节、假设检验的常用方法

（一）置信区间法。

（二）临界值法。

（三）P值法。

第三节、正态总体期望值的假设检验

（一）总体方差已知条件下的u检验。

（二）总体方差未知条件下的t检验。

第四节、正态总体方差的检验

（一）单个正态总体方差的检验。

（二）两个正态总体的方差齐性F检验。

第五节、分类资料的检验

列联表资料的检验。

三、考核知识点和要求

（一）、假设检验的基本思想

识记：小概率原理，两类错误。

应用：假设检验的一般步骤，

（二）、假设检验的常用方法

识记：置信区间法。

应用：临界值法，P值法。

（三）、正态总体期望值的假设检验

应用：方差已知条件下的u检验，方差未知条件下的t检验。

（四）、正态总体方差的检验

应用：单个正态总体方差的检验，两个正态总体的方差齐性F检验。

（五）、分类资料的检验

识记：列联表资料的检验。

III. 考试形式及试卷结构

1. 闭卷笔试(可以使用计算器); 全卷满分100分, 考试时间为150分钟。
2. 试卷题型比例：选择题、填空题约占60%；计算题 约占40%。

3、试卷内容比例：概率论内容约60%，数理统计内容约40%。其中试题易、中、难题目各占40%、50%、10%。

IV. 参考书目

1、《医药数理统计方法》（第一版），祝国强主编，高等教育出版社。

2、《医药数理统计方法》（第三版），刘定远主编，人民卫生出版社。

                          （广东药学院龙洪波，黄榕波，楚慧珠，庄锦才编）

V. 题型示例

10、已知随机变量X服从二项分布，且E（X）=2.4、V（X）=1.44，则二项分布的参数n，P的值为（  ）

A．n=4，P=0.6      B. n=6，P=0.4      C. n=8，P=0.3      D. n=24，P=0.1

三、计算题（40分）

1、 设20支针剂中有4支不合格品。今从中任取3支，求下列事件的概率。（8分）

①恰好有2支不合格品     ②没有不合格品      ③至少有一支不合格品。

２、设随机变量X的分布列如下：

求 ① 常数Ｃ　②数学期望 Ｅ（Ｘ）　③ 方差 Ｖ（Ｘ）  （8分）

3、测定某药物对血浆的凝血时间，抽取 9份血浆，经计算得：样本均数为2.125，标准差为0.017；，假定该药对血浆的凝血时间服从正态分布，试求出总体均数的置信度为95%的置信区间。（8分）

4、某药厂生产复方维生素，要求每50g维生素含铁2400mg。现从某批生产过程中随机抽取部分试样，进行 9 次测定，得铁的含量(mg/50g)；经计算得到样本均数为2451，样本标准差为 29.766, 若该批产品铁含量服从正态分布，试判断这批产品的含铁量是否合格。（α＝0.05）

对于某产品的不合格率按三个工人分层统计结果如下：

问不合格率是否与人员不同有关系？